※第21〜25章の議論はこの『音楽教程』全体の中で私が最も面白いと思った部分です. この部分でボエティウスはオクターヴが〈二倍比〉,5度が〈$2$ の単部分超過比〉,4度が〈$3$ の単部分超過比〉であることを証明しようとしています.
これを初めて読んだときは,オクターヴが〈二倍比〉云々を証明するというので「それって定義じゃないの?」「定義されたものを証明するってどういうこと?」と思ったのですが,よくよく読んでみると,第一巻16章で与えられたオクターヴ,5度,4度の数比による定義から導き出された性質を用いて,今度は逆にその性質を満たすものは最初に定義した数比しかありえないことが詳しく論証されているのでした. これには感動しました. このことを説明したくてこの文書を書き始めたと言ってよいです.
すべての中で最上のものであるオクターヴの協和が〈多倍比〉の類であり,二倍であることが証明されるであろう. この証明のための準備として次の命題を示す.
命題1 あらゆる〈単部分超過比〉から,それに続く〈単部分超過比〉が引かれるとき,残ったものは引かれた比の半分より小さい.
例 〈$2$ の単部分超過比〉から〈$3$ の単部分超過比〉を引くと〈$8$ の単部分超過比〉であるが,これは〈$3$ の単部分超過比〉の半分より小さい.
なぜなら,〈$3$ の単部分超過比〉$\displaystyle 4:3 = \frac{4}3:1$ の幾何中項は $\displaystyle \sqrt{\frac{4}3}$ なので $\displaystyle \frac{4}3:1$ の半分は $\displaystyle \sqrt{\frac{4}3}:1$ となる. 一方 $\displaystyle \frac{9^2}{8^2}=\frac{81}{64}<\frac{4}3$ なので $\displaystyle \frac{9}{8}<\sqrt{\frac{4}3}$ となり 〈$8$ の単部分超過比〉は〈$3$ の単部分超過比〉の半分より小さい.
命題1は次のように言い換えられる.
命題2 $a$ を3以上の整数とする. $a:a-1$ から $a+1:a$ を引いたものは $a+1:a$ の半分より小さい.
証明 $a:a-1$ から $a+1:a$ を引くと $a^2:(a-1)(a+1)=a^2:a^2-1$.
$a+1:a$ の幾何中項は $\sqrt{a(a+1)}$ なので $a+1:a$ の半分は $\sqrt{a(a+1)}:a = \sqrt{a+1}:\sqrt{a}$.
したがって,示すべきことは \[ \frac{a^2}{a^2-1}<\sqrt{\frac{a+1}{a}}\quad\cdots (*) \]
また $\displaystyle (*) \Leftrightarrow \left(\frac{a^2}{a^2-1}\right)^2<\frac{a+1}a \Leftrightarrow \frac{a+1}{a}\cdot\frac{(a^2-1)^2}{a^4}>1$. さらに \[ \frac{a+1}{a}\cdot\frac{(a^2-1)^2}{a^4} = \frac{a^5+a^4-2a^3-2a^2+a+1}{a^5} =1+\frac{a^4-2a^3-2a^2+a+1}{a^5} \] したがって $\displaystyle (*)\Leftrightarrow \frac{a^4-2a^3-2a^2+a+1}{a^5}>0$.
$a\geqq 3$ のとき直前の不等式の左辺の分母 $a^5$ は正であるので, $a^4-2a^3-2a^2+a+1>0$ を示せばよい.
$f(a)=a^4-2a^3-2a^2+a+1$ とする. \[ f(a)=a^4-2a^3-2a^2+a+1=a^2(a^2-2a-2)+a+1=a^2\{(a-1)^2-3\}+a+1 \] $(a-1)^2-3$ は $a$ の関数として $a\geqq1$ の範囲で増加関数. したがって $f(a)$ も $a\geqq1$ の範囲で増加関数. $f(3)=13>0$ なので $a\geqq 3$ のとき $f(a)>0$. QED.
※『音楽教程』の本文には命題の一般的な証明は書いていないので自分で証明をつけましたが,ボエティウスはどう理解していたのでしょうね?
この章からの議論を始める前に,オクターヴ,5度,4度の性質について確認しておくことがあります. まず第一巻の要約にまとめた音程関係について
以上の関係から次が得られます.
★ 2つの4度ー5度=全音+半音
なぜなら
2つの4度ー5度=2つの4度ー(4度+全音)=4度ー全音
=(2全音+半音)ー全音=全音+半音
さらに次のことが議論の前提になります.上の i, ii, iii と合わせて,ここでの議論の公理といってもよいものです.
オクターヴが〈多倍比〉であることを背理法によって証明する.
5度,4度,そして全音が〈単部分超過比〉であることを順に証明する.
命題1 4度は〈多倍比〉でなく,〈単部分超過比〉である.
証明 4度が〈多倍比〉であると仮定する.このとき,5度は4度より大きい協和なので, v, vi より5度も〈多倍比〉である.
4度が〈二倍〉なら, vi より5度は〈三倍〉. ii より全音は5度($3:1$)から4度($2:1$)を引いたものなので $3:2$, つまり〈$2$ の単部分超過比〉.
すると二全音は $3^2:2^2=9:4$ となり〈二倍〉より大きいので,二全音が4度より大きいことになり矛盾.
次に $n$ を $3$ 以上の整数とし,4度が〈$n$ 倍〉だったと仮定すると, vi より5度は〈$n+1$ 倍〉である. 全音は5度から4度を引いたものなので $n+1:n$, すなわち〈$n$ の単部分超過比〉である.
このとき三全音は $(n+1)^3:n^3$ であるが,これは〈$n$ 倍〉よりも小さいことが次のように示せる. まず \[ \frac{(n+1)^3}{n^3}=\frac{n^3+3n^2+3n+1}{n^3}=1+\frac{3}{n}+\frac{3}{n^2}+\frac{1}{n^3}. \] $n\geqq 3$ なら,右辺は $n=3$ のとき最大になるので \[ \frac{(n+1)^3}{n^3}=1+\frac{3}{n}+\frac{3}{n^2}+\frac{1}{n^3}\leqq 2+\frac{1}3+\frac{1}{27}<3 \leqq n. \] したがって $(n+1)^3:n^3$ の三全音は〈$n$ 倍〉の4度よりも小さいことになるが, iii より4度は二全音+半音なので矛盾である.
以上より,4度は〈多倍比〉でない. QED.
命題2 5度は〈多倍比〉でなく,〈単部分超過比〉である.
証明 5度が〈多倍比〉であると仮定する. 命題1より4度は〈単部分超過比〉であり, vi より5度と4度は連続するので,5度は〈二倍比〉,4度は〈$2$ の単部分超過比〉でなければならない.
このとき全音は5度($2:1$)から4度($3:2$)を引いた音程なので,$4:3$, すなわち 〈$3$ の単部分超過比〉である.
すると二全音は $4^2:3^3=16:9$ となるが,これは $3:2$,すなわち〈$2$ の単部分超過比〉より大きい. これは二全音が4度より大きいことを意味し,矛盾である.QED.
命題3 全音は〈単部分超過比〉である.
証明 命題1,命題2, vi より,5度と4度は連続した〈単部分超過比〉でなければならないので,5度が〈$n$ の単部分超過比〉,4度が〈$n+1$ の単部分超過比〉であるような $2$ 以上の整数 $n$ が存在する.
全音は5度($n+1:n$)から4度($n+2:n+1$)を引いた音程なので,その比は \[ (n+1)^2:n(n+2)=(n^2+2n+1):(n^2+2n) \] すなわち〈$n^2+2n$ の単部分超過比〉である.QED.
5度が〈$2$の単部分超過比〉,4度が〈$3$の単部分超過比〉であることを示す.
i より5度+4度はオクターヴであり,第22章よりそれは〈多倍比〉である.
前と同様に,命題1,命題2, vi より,5度が〈$n$ の単部分超過比〉,4度が〈$n+1$ の単部分超過比〉であるような $2$ 以上の整数 $n$ が存在する.
オクターヴは5度($n+1:n$)と4度($n+2:n+1$)を足したものなので, \[ (n+1)(n+2):n(n+1)=n+2:n=\left(1+\frac{2}n\right):1 \] という比で表されるが,これは $n\geqq 3$ のとき〈多倍比〉ではなく, $n=2$ のとき〈二倍比〉である.
したがって5度は〈$2$の単部分超過比〉,4度は〈$3$の単部分超過比〉であり,オクターヴは〈二倍比〉である.
5度は〈$2$の単部分超過比〉,4度は〈$3$の単部分超過比〉であることは前章で示した.
全音は5度($3:2$)から4度($4:3$)を引いたものなので \[ 3\times3:2\times 4=9:8 \] の比で表され,それは〈$8$の単部分超過比〉である.
オクターヴは $2:1$, 5度は $3:2$ なので,オクターヴ+5度は $2\times3:2=3:1$ すなわち〈三倍比〉.
オクターヴ+5度に4度を組み合わせると2オクターヴになるので,$3:1$ と $4:3$ で表される音程を足した音程は $4:1$ であらわされる. つまり2オクターヴは〈四倍比〉である.
オクターヴは $2:1$, 4度は $4:3$ なので,オクターヴ+4度は $2\times4:3=8:3$ で表される. $8:3$ は〈複部分超過比〉であり,〈多倍比〉でも〈単部分超過比〉でもないので, v よりこれは協和ではない.
このことについてのプトレマイオスの見解については後述する.(第5巻)
半音と名付けられているのは,真に全音の半分であるものではなく,全音に満たないものであり,その広がりは,往時の人々においてはリンマあるいはディエシスと呼ばれていたものである.
4度から全音二つが引かれたものが半音である.
※半音の比は以前のページで求めましたがもう一度やっておきます. 全音は $9:8$ なので,二全音は $9^2:8^2=81:64$ で表されます. $4:3$ の4度から $81:64$ の二全音を引くと, \[ 4\times64:3\times81=256:243 \] が,半音を表します. 以下原文の求め方を辿ります.
$243:256$ の距離が全音の完全な半分の幅でないことを証明しよう.
※これも以前のページで示しましたが,原文の議論を辿ることにしたいと思います. 原文では,後の第三巻1章で証明されることを使います. それは次の命題です.
命題 $9:8=18:16$ は全音を表していた.$18:17:16$ を考えよう. すると $18:17$ は全音の半分より小さく,$17:16$ は全音の半分より大きい.
証明 $\displaystyle 18:17=\left(1+\frac{1}{17}\right):1$, $\displaystyle 17:16=\left(1+\frac{1}{16}\right):1$ であり,$\displaystyle \frac{1}{17}<\frac{1}{16}$ なので,$18:17$ は $17:16$ より小さい. また $18:17$ と $17:16$ は全音を二つに分けており,二つの部分は等しくなく $18:17$ の方が小さいので, $18:17$ は全音の半分より小さく,$17:16$ は全音の半分より大きい.QED.
$256-243=13$ である. $13$ の $18$ 倍は $234$ で $243$ より小さく,$13$ の $19$倍は $247$ で $243$ より大きい.これより次の不等式が得られる \[ \frac1{19}=\frac{13}{247}<\frac{13}{243}<\frac{13}{234}=\frac{1}{18}. \]
したがって $\displaystyle 256:243 =\left(1+\frac{13}{243}\right):1$ は $\displaystyle \left(1+\frac{1}{19}\right):1$ より大きく,$\displaystyle \left(1+\frac{1}{18}\right):1$ より小さい.
一方上の命題より,全音の半分は $\displaystyle \left(1+\frac{1}{17}\right):1$ より大きく,$\displaystyle \left(1+\frac{1}{16}\right):1$ より小さい.
$\displaystyle \left(1+\frac{1}{17}\right):1$ は $\displaystyle \left(1+\frac{1}{18}\right):1$ より大きいので,$256:243$ は全音の半分より小さい.
※要するに,これまで出てきた比を小さい方から大きい方へ順番に並べると次のようになります. \[ 20:19,\quad 256:243,\quad 19:18,\quad 18:17,\quad \text{全音の半分},\quad 17:16 \]
$243:256$ を二度続けた比を考えよう. \[ 243^2:243\times256:256^2=59049:62208:65536 \] したがって二半音は $65536:59049$ で表される. これは全音より小さい.なぜなら \[ 9:8 =59049\left(1+\frac{1}{8}\right):59049 = 66430.125:59049 \] は $65536:59049$ より大きいから.
全音から半音を引いた残りはギリシア人によってアポトメーと呼ばれる. われわれによっては「切り分けること decisio」と呼ばれうるものである.
半音は全音の半分に満たないので,アポトメーは全音の半分より大きい.
全音は $8:9$, 半音は $243:256$ なので,$8:x:9$ において $8:x$ が $243:256$ になるように $x$ を取ると $x:9$ がアポトメーの比である. \[ 8:8\times\frac{256}{243}:9 = 1944:2048:2187 \] なのでアポトメーの比は$2048:2187$.
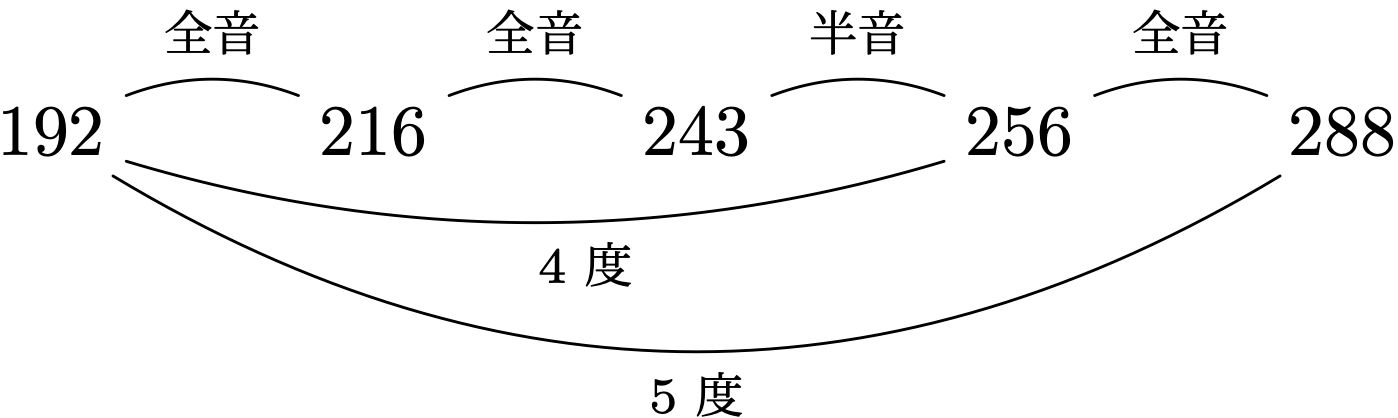
$192:216=216:243=8:9$, $192:256=3:4$ なので, $192:216:243:256$ の比は 全音+全音+半音=4度 を表す(第28章). $\displaystyle 256\times\frac{9}{8}=288$ であり,$192:288=2:3$ なので 5度=4度+全音=3全音+半音 である.

4度+5度=オクターヴなので,オクターヴは5全音+2半音からなる. 2半音は全音より小さいので,オクターヴは6全音より小さい.
6全音を表す6つの〈$8$ の単部分超過比〉の列を見出そう.
※このような列を得るここでの基本的なアイデアは第8章と同じですが,手順は少しだけ異なります.
まず8倍の列 $1,8,64,512,4096,32768,262144$ を考える.
$262144$ にその $1/8$ の $32768$ を足すと $294912$ となり,$262144:294912=8:9$ は〈$8$ の単部分超過比〉である.
次に $294912$ にその $1/8$ の $36864$ を足すと $331776$ となり,$294912:331776=8:9$ は〈$8$ の単部分超過比〉である.
この操作を繰り返し,次の表を得る.
| 8倍 | 8の単部分超過比 | 1/8 | |||||
| 1 | 8 | 64 | 512 | 4096 | 32768 | 262144 | 32768 |
| 294912 | 36864 | ||||||
| 331776 | 41472 | ||||||
| 373248 | 46656 | ||||||
| 419904 | 52488 | ||||||
| 472392 | 59049 | ||||||
| 531441 | |||||||
したがって6全音は $531441:262144$ で表される. 一方オクターヴは $2:1=524288:262144$ なので,確かに6全音はオクターヴより大きい.
6全音とオクターヴの差をコンマと呼ぶ.コンマは $531441:524288$ の比で表される.
いまや私は,読者の不快感を回避するために,この巻を閉じるべきであろう.